SOCI 620: Quantitative methods 2

Welcome

Introduction &
course structure

  1. Introductions
  2. Course motivation
  3. Roadmap
  4. Logistics
  5. Software and computer setup
  6. Hands-on: R and RMarkdown

Slides are licensed under CC BY-NC-SA 4.0

Land acknowledgement

McGill University is located on land which has long served as a site of meeting and exchange amongst Indigenous peoples, including the Haudenosaunee and Anishinabeg nations. McGill honours, recognizes and respects these nations as the traditional stewards of the lands and waters on which we meet today.

https://www.mcgill.ca/fph/welcome/traditional-territory

see also:

Chelsea Vowel. “Beyond Territorial Acknowledgments.” Âpihtawikosisân (blog), September 23, 2016. https://apihtawikosisan.com/2016/09/beyond-territorial-acknowledgments/.

Intro­duc­tions

Photo of a large number of arms extended into the center of the frame, many of which are shaking hands as in greeting.

Course motivation

Close-up photo of a few puzzle pieces, each of which shows a piece of an inscrutable (possibly technical) image.

Unpacking regressions

Linear regression (OLS):

A scatter plot with a trend line drawn through the center. Each of the points has a dotted line tracing the vertical offset from the trend line.

Unpacking regressions

Linear regression (OLS):

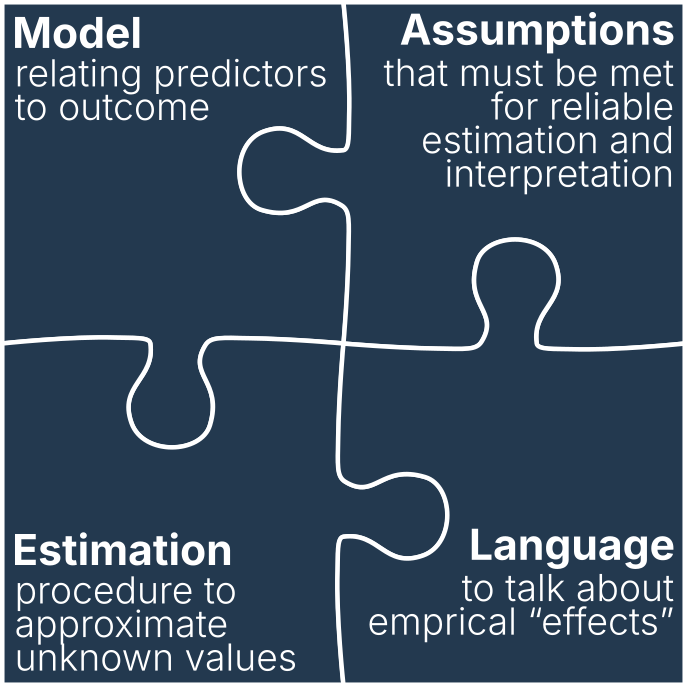
A graphic composed of four interlocking, labeled puzzle pieces. Piece 1: 'Model relating predictors to outcome'; Piece 2: 'Assumptions that must be met for reliable estimation and interpretation'; Piece 3: 'Estimation procedure to approximate unknown values'; Piece 4:'Language to talk about empirical effects'

Unpacking regressions

A single puzzle piece labeled 'Model relating predictors to outcome'
  • As social scientists, the model is what we really care about
    A ‘mental map’ of your theoretical argument
  • Also the fun part
    Building a tiny working model of the social world
  • OLS (like all models) comes with very specific ideas about what can matter in the social world and how those things can be related
    Abbott (1988):Transcending general linear reality
A single puzzle piece labeled 'Model relating predictors to outcome'
  • Predictions and measures from model and data
  • Technical procedures
    Important, but less sociological
  • Ordinary least squares (OLS)
  • But also: maximum likelinhood (ML); maximum a-posteriori (MAP); Markov chain Monte-Carlo (MCMC); …

Probability models

We will use the lens of probability models to describe all of the models in the class.

Intuitive

  • Probability distributions help to break models into components
  • Probability distributions provide an intuitive language for discussing uncertainty

Flexible

  • Probability distributions describe the uncertainties in the social processes you are studying
  • Simple algebra fits these distributions together to make a model that supports your claims
Children's building toy of steel balls and magnetic plastic rods. They have been arranged into the crude shape of a flower, a sun, and a bird in flight.

Bayesian vs. frequentist statistics

Probability models are often associated with “Bayesian” statistics, which itself is often contrasted with “Frequentist” statistics. What do those terms mean?

Frequentist

Bayesian

Philosophical contrasts

  • The probability of an event is the proportional frequency of that event across the entirety of a given ‘context’
  • The probability of an event is is a rigorous way to quantify subjective uncertainty about that event

Practical contrasts

  • Significant limitations on types of models that can be used
  • Fast computation of estimates for those models (OLS, ML, …)
  • Diffcult to talk about level of confidence in estimates
  • Easy to work with a wide range of models
  • Estimation is computationally “expensive” (MCMC, Hamiltonian MC, …)
  • (Arguably) easy to talk about confidence in estimates
  • Need to specify prior beliefs (more on this later)

In practice, these differences usually remain “under the hood.” Either approach can be used with no significant impact on reliability or credibility.
I strongly advocate for a pragmatic approach: use whichever framing makes the most sense for your specific model, data, resources, and audience.

Roadmap

Old map of a part of Prussia

Roadmap

Part 1: Parametric probability models

  • Social-scientific models as random processes
  • Overview of probability distributions
  • Estimating parameters

Part 2: Linear models and model checking

  • Re-framing linear regression as probability model
  • General model considerations (causality, overfitting)

Part 3: Generalized linear models

  • Expanding linear models with outcome distributions and link functions
  • Binary, count, and categorical outcomes

Part 4: Complications in data and estimation

  • Missing data and weighted observations

Part 5: Multilevel models

  • Two-level models (nested data)
  • Covariance structures
  • Generalized multilevel models

Part 6: Building more complex models

  • Probability models for other processes

Logistics

Black and white photo of two large metal gears interlocking

Schedule

Syllabus

Class periods

  • Lecture and discussion
    Formal discussion of topics
  • Usually finish with demos
    Working in R
  • Laptop will be necessary

Labs

  • Work through example code with TA
  • Work on assignments/projects in the same space as one another (study hall)
    Ask questions, consult, commiserate
  • Once per week

Assessments

Worksheets

  • Five worksheets over the semester
    Due dates on syllabus
  • Distributed as RMarkdown templates to complete
  • Everyone will evaluate two of their peers for each worksheet using FeedbackFruits
  • Turn in through MyCourses
  • Working together is fine (encouraged, even!), but each person needs to create their own writeup of code and expproseosition

Research project

  • The main item is an original research project
  • Due in four parts (the four "P"s):
    Precis; proposal; presentation; paper
  • Ideally, will be part of a larger research project
    E.g. a draft of the methods section for a dissertation chapter?
  • Meet with me early in the semester to discuss your topic ideas

Generative AI

an IBM selectric typewriter

“Generative AI”

  • Language models that predict subsequent “tokens” based on previous text.
  • E.g. Microsoft Copilot (provided by McGill) OpenAI’s ChatGPT, Google’s Gemini, Meta’s Llama, etc.

The use of these tools is strongly discouraged

  • They are bad for the world.
  • They are bad for students.

Generative AI is bad for the world

Environmental impact

Photo of an oil refinery in a blighted landscape

Human exploitation

Generative AI is bad for students

“Typical” text

  • The technology that makes generative AI work is essentially like the predictive text on your phone, but trained on as much of the internet as corporations can get their hands on.
    One thousand Redditors (or Github projects) in a trenchcoat
  • The models are trained solely to sound unsurprising, not to recognize important or interesting ideas.
    “When ChatGPT summarises, it actually does nothing of the kind”

Writing is its own end

Generated image of a generic middle-aged white man in front of a black background looking at the camera. His eyes are in sharp focus, other parts of his face are blurry, and everything besides his face is very blurry.

Tools & resources

Microsoft Teams

  • Available at this link through browser or app
  • Q&A and discussions (ask and answer!)
  • Best place to contact me
  • Let me know if you have trouble with access

MyCourses

  • Turning in assignments
  • FeedbackFruits for peer assessment

Readings

Software

The R language

  • Class, labs, and worksheets will use R
  • Open source (free forever)
  • Vibrant ecosystem of add-on packages
  • De facto standard for scholarly statistics

RMarkdown

  • Plain-text format to incorporate R code into documents
  • Converts to Word, PDF, HTML, …
  • (Quarto is very similar to RMarkdown)

RStudio (optional)

  • A convenient interface to R and RMarkdown
  • Made by Posit, the “opinionated” company behind tidyverse
  • Alternatives:
    VSCode (VSCodium) from Microsoft;
    or any text editor and terminal

RStudio (or VSCode)
User-friendly interface to
the R environment and
RMarkdown

R
Statistical language and
environment (the ‘engine’
of your analysis)

rethink­ing

Textbook companion package

brms
R package for Bayesian model estimation

lme4
R package for mulilevel GLM estimation

…
Other R packagages (tidyverse, data.table, ggplot, …)

stan
General-purpose software for MCMC estimation

Software

Installing

Testing

  • A simple script to test the rethinking installation is at:
    https://soci620.netlify.app/labs/lab_1.R

  • You can download and run this, copy and paste it, or run the whole thing from directly in R:

    source("https://soci620.netlify.app/labs/lab_1.R")

Image credit

Photo of a large number of arms extended into the center of the frame, many of which are shaking hands as in greeting.

Photo by Marlis Trio Akbar on Unsplash

Close-up photo of a few puzzle pieces, each of which shows a piece of an inscrutable (possibly technical) image.

Photo by John Hritz on Flickr

A scatter plot with a trend line drawn through the center. Each of the points has a dotted line tracing the vertical offset from the trend line.

R script to produce figure

Children's building toy of steel balls and magnetic plastic rods. They have been arranged into the crude shape of a flower, a sun, and a bird in flight.

Playmatey magnetic building blocks via WorthPoint

Old map of a part of Prussia

Coloured engraving by S.J. Neele after L. Hebert. Wellcome Collection.

Black and white photo of two large metal gears interlocking

Photo by Natasha Wheatland on Flickr

an IBM selectric typewriter

Photo by Wikimedia user Etan J. Tal

Photo of an oil refinery in a blighted landscape

Photo by Patrick Hendry on Unsplash

Generated image of a generic middle-aged white man in front of a black background looking at the camera. His eyes are in sharp focus, other parts of his face are blurry, and everything besides his face is very blurry.

Faces of 500 professional golfers, averaged by Reddit user u/osmutiar/

- performativity - what does saying "honours, recognizes, and respects" *do*? - How does McGill act toward Indigenous communities (local and distant) outside of this statement? - This class -- we'll talk about the role of science in colonial oppression. - What does a statement like this mean for us as the McGill community? As members of this class?

Small class icebreaker - Names - experience with R - Are you already working with a dataset for your thesis or dissertation?

The "linear regression" is a workhorse of social science statistics. It gives us a standard way to relate two variables to each other (and control for other confounding variables) It's great for research because it's a flexible way to talk about quantitative results that allows us to "black box" a lot of complexity into discussion of _coefficients_, _statistical significance_, etc. BUT, linear regressions incorporate a lot of different components in that black box!

Each of these is it's own thing, and can be (in theory) swapped out for something else. (Of course, there are dependencies! Assumptions depend on model and vice versa, e.g.)

In this class we'll be focusing on the models. But in the process we'll look at various ways of estimating those models

We'll use both approaches in this class, though the model descriptions will tend toward the Bayesian